Model regresi disebut sebagai model yang baik jika model tersebut memenuhi asumsi-asumsi klasik yaitu multikolinieritas, autokorelasi, heteroskedastisitas dan normalitas.
Proses pengujian asumsi klasik menggunakan SPSS dilakukan bersamaan dengan proses uji regresi sehingga langkah-langkah menggunakan langkah kerja yang sama dengan uji regresi.
Untuk memahami pengertian uji asumsi klasik dapat disimak pada laman ini, untuk memahami pengertian regresi simak pada laman ini, sedangkan langkah SPSS regresi simak di laman ini.
Kasus:
- Merek (X1), layanan (X2) dan harga (X3) terhadap pembelian (Y)
- N = 34
INPUT DATA
 |
| Gambar 1 |
Gambar 1 (klik untuk perbesar) adalah potongan penampakan spreadsheets Data View SPSS. Dengan demikian kita memliki 4 kolom variabel yaitu X1, X2, (X3) dan Y. Pada tahap ini input data sudah selesai. Lanjut langkah perintah uji.
LANGKAH-LANGKAH
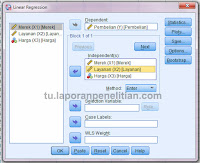
- Klik Analyze - Regression - Linear...
- Pindahkan Pembelian (Y) ke Dependent, disusul masukkan merek (X1), layanan (X2) dan harga (X3) ke Independent(s)
- Klik Statistics. Pilih Estimate, Covariance matrix, Model fit, Collinearity diagnostics dan Durbin-Watson. Klik Continue.
- Klik Plots. Masukkan *SRESID ke Y dan *ZPRED ke X. Klik Continue.
- Klik OK
 |
| Gambar 2 |
Pada tahap ini langkah uji regresi sudah selesai dan kita sudah memiliki output. Langkah selanjutnya adalah mengambil keputusan berdasarkan hasil output tersebut.
PENGAMBILAN KEPUTUSAN
[Download Output Pdf 102 KB] dan [Download Tabel Durbin-Watson Pdf 175 KB]
Klik link di atas untuk download output. Di dalam output tersebut berisi hasil-hasil pengujian regresi berdasarkan formula yang telah ditetapkan yaitu 3 variabel bebas dan 1 variabel tergantung.
Multikolinieritas
Model regresi bebas dari masalah multikolenieritas apabila nilai Tolerance lebih dari 0,10 dan nilai VIF kurang dari 10 yang berarti tidak ada korelasi antar variabel bebas.
Lihat output pada kotak Coefficients. Semua nilai Tolerance di atas 0,10 dan nilai VIF kurang dari 10 sehingga disimpulkan bahwa model regresi bebas dari multikolenieritas.
Autokorelasi
Model regresi bebas dari masalah autokorelasi apabila nilai Durbin-Watson hitung antara dU dan 4-dU yang berarti tidak memiliki korelasi antara variabel pengganggu pada periode tertentu dengan variabel pengganggu periode sebelumnya.
Download Tabel Durbin-Watson dan lihat kolom k (jumlah variabel independen) dan baris n jadi 3 dan 34. Nilai dU tabel sebesar 1,6519 sehingga batasnya antara dU dan 4-dU (1,6519 dan 2,3481).
Lihat output pada kotak Model Sumary terlihat nilai Durbin-Watson hitung sebesar 2,251 sehingga diputuskan bahwa tidak terdapat autokorelasi dalam model regresi.
Heteroskedastisitas
Model regresi yang baik adalah homoskedastisitas atau tidak terjadi heteroskedastisitas yaitu titik-titik pada Scatterplot menyebar di atas dan di bawah atau di sekitar 0 serta tidak membentuk pola tertentu.
Lihat Scatterplot pada output terlihat titik-titik menyebar antara -2 hingga 1 dan tidak membentuk pola tertentu sehingga disimpulkan model regresi adalah homoskedastisitas atau tidak heteroskedastisitas.
Normalitas
Analisis regresi adalah statistik parametrik sehingga model regresi yang valid jika data berdistribusi normal yaitu titik-titik pada grafik P-P Plot menyebar di sekitar garis diagonal.
Lihat P-P Plot pada output terlihat titik-titik menyebar di sekitar garis diagonal sehingga diputuskan model regresi berdistribusi normal. Untuk estimasi normalitas dapat diketahui menggunakan Kolmogorov-Smirnov Test.
sumber http://tu.laporanpenelitian.com/2015/06/95.html
Tidak ada komentar:
Posting Komentar