Tutorial Olah Data SPSS : Uji Normalitas Kolmogorov-Smirnov

Tutorial Penelitian ~ Uji normalitas Kolmogorov-Smirnov adalah uji yang bertujuan untuk mengetahui apakah data dalam variabel yang akan dianalisis berdistribusi normal.

Data yang baik dan layak digunakan dalam penelitian adalah data yang memiliki distribusi normal. Data berdistribusi normal artinya data mempunyai sebaran merata sehingga benar-benar mewakili populasi.

Uji normalitas data dilakukan sebelum data diolah berdasarkan model-model penelitian. Uji normalitas adalah membandingkan antara data yang akan diteliti dengan data berdistribusi normal berdasarkan mean dan standar deviasi.

Jika data berdistribusi normal maka analisis statistik dapat memakai pendekatan parametrik, sedangkan jika data tidak berdistribusi normal maka analisis menggunakan pendekatan non-parametrik.

Kasus:

• N = 10
• Berat Badan (Skala Rasio)

---

INPUT DATA

Gambar 1

Input data ke spreadsheets Microsoft Excel kemudian copy dan paste ke spreadsheets Data View SPSS dilanjutkan dengan input parameter deskripsi ke spreadsheets Data Variable SPSS.

Gambar 1 (klik untuk perbesar) adalah penampakan spreadsheets Data View SPSS. Dengan demikian kita memliki 1 kolom variabel. Pada tahap ini input data sudah selesai. Lanjut langkah perintah uji.

---

LANGKAH-LANGKAH

1. Klik Analyze - Nonparametrik Test - Legacy Dialogs - 1-Sample K-S
2. Pindahkan Berat Badan ke Test Variable List
3. Klik OK

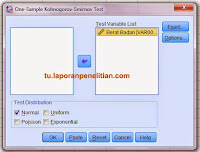Gambar 2

Gambar 2 (klik untuk perbesar) adalah menu popup pada saat Anda melakukan langkah ke-2 dan ke-3 yaitu memilih variabel yang akan dianalisis.

Pada tahap ini uji normalitas sudah selesai dan kita sudah mendapatkan output SPSS. Langkah selanjutnya adalah mengambil keputusan berdasarkan output tersebut.

---

PENGAMBILAN KEPUTUSAN

• Jika Sig di atas 0,05 maka berdistribusi normal
• Jika Sig di bawah 0,05 maka tidak berdistribusi normal

Gambar 3

Gambar 3 (klik untuk perbesar) adalah output hasil uji normalitas Kolmogorov-Smirnov. Output menujukkan bahwa nilai Asymp. Sig. (2-tailed) sebesar 0,960 maka lebih besar dari 0,05 sehingga data berat badan berdistribusi normal.
http://tu.laporanpenelitian.com/2015/05/63.html